编译原理(紫龙书)中文第2版习题答案
- 前言
- Exercises for Section 1.1
- Exercises for Section 1.3
- Exercises for Section 1.6
- Exercises for Section 2.2
- Exercises for Section 2.3
- Exercises for Section 2.4
- Exercises for Section 2.6
- Exercises for Section 2.8
- 第2章要点
- Exercises for Section 3.1
- Exercises for Section 3.3
- Exercises for Section 3.4
- Exercises for Section 3.5
- Exercises for Section 3.6
- Exercises for Section 3.7
- Exercises for Section 3.8
- Exercises for Section 3.9
- 第3章要点
- Exercises for Section 4.2
- Exercises for Section 4.3
- Exercises for Section 4.4
- Exercises for Section 4.5
- Exercises for Section 4.6
- Exercises for Section 4.7
- 第4章要点
- Exercises for Section 5.1
- Exercises for Section 5.2
- Exercises for Section 5.3
- Exercises for Section 5.4
- Exercises for Section 5.5
- Exercises for Section 6.1
- Exercises for Section 6.2
- Exercises for Section 6.3
- Exercises for Section 6.4
- Exercises for Section 6.5
- Exercises for Section 6.6
- Exercises for Section 6.7
- Exercises for Section 7.2
- Exercises for Section 7.3
- Exercises for Section 7.4
- Exercises for Section 7.5
- Exercises for Section 7.6
- Exercises for Section 7.7
- Exercises for Section 8.2
- Exercises for Section 8.3
- Exercises for Section 8.4
- Exercises for Section 8.5
- Exercises for Section 12.3
Exercises for Section 4.2
4.2.1
Consider the context-free grammar:
S -> S S + | S S * | aand the string aa + a*.
- Give a leftmost derivation for the string.
- Give a rightmost derivation for the string.
- Give a parse tree for the string.
- ! Is the grammar ambiguous or unambiguous? Justify your answer.
- ! Describe the language generated by this grammar.
Answer
-
S =lm=> SS* => SS+S* => aS+S* => aa+S* => aa+a*
-
S =rm=> SS* => Sa* => SS+a* => Sa+a* => aa+a*
-
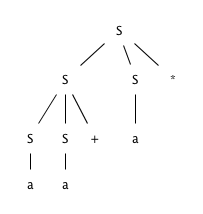
-
Unambiguous
-
The set of all postfix expressions consist of addition and multiplication
4.2.2
Repeat Exercise 4 . 2 . 1 for each of the following grammars and strings:
-
S -> 0 S 1 | 0 1 with string 00011l.
-
S -> + S S | * S S | a with string + * aaa.
-
! S -> S (S) S | ε with string (()())
-
! S -> S + S | S S | (S) | S * | a with string (a+a)*a
-
! S -> (L) | a 以及 L -> L, S | S with string ((a,a),a,(a))
-
!! S -> a S b S | b S a S | ε with string aabbab
-
The following grammar for boolean expressions:
bexpr -> bexpr or bterm | bterm bterm -> bterm and bfactor | bfactor bfactor -> not bfactor | (bexpr) | true | false
Answer
- S =lm=> 0S1 => 00S11 => 000111
- S =rm=> 0S1 => 00S11 => 000111
- Omit
- Unambiguous
- The set of all strings of 0s and followed by an equal number of 1s
2、
- S =lm=> +SS => +*SSS => +*aSS => +*aaS => +*aaa
- S =rm=> +SS => +Sa => +*SSa => +*Saa => +*aaa
- Omit
- Unambiguous
- The set of all prefix expressions consist of addition and multiplication.
3、
- S =lm=> S(S)S => (S)S => (S(S)S)S => ((S)S)S => (()S)S => (()S(S)S)S => (()(S)S)S => (()()S)S => (()())S => (()())
- S =rm=> S(S)S => S(S) => S(S(S)S) => S(S(S)) => S(S()) => S(S(S)S()) => S(S(S)()) => S(S()()) => S(()()) => (()())
- Omit
- Ambiguous
- The set of all strings of symmetrical parentheses
4、
- S =lm=> SS => S*S => (S)*S => (S+S)*S => (a+S)*S => (a+a)*S => (a+a)*a
- S =rm=> SS => Sa => S*a => (S)*a => (S+S)*a => (S+a)*a => (a+a)*a
- Omit
- Ambiguous
- The set of all string of plus, mupplication, 'a' and symmetrical parentheses, and plus is not the beginning and end of the position, multiplication is not the beginning of the position
5、
- S =lm=> (L) => (L, S) => (L, S, S) => ((S), S, S) => ((L), S, S) => ((L, S), S, S) => ((S, S), S, S) => ((a, S), S, S) => ((a, a), S, S) => ((a, a), a, S) => ((a, a), a, (L)) => ((a, a), a, (S)) => ((a, a), a, (a))
- S =rm=> (L) => (L, S) => (L, (L)) => (L, (a)) => (L, S, (a)) => (L, a, (a)) => (S, a, (a)) => ((L), a, (a)) => ((L, S), a, (a)) => ((S, S), a, (a)) => ((S, a), a, (a)) => ((a, a), a, (a))
- Omit
- Unambiguous
- Something like tuple in Python
6、
- S =lm=> aSbS => aaSbSbS => aabSbS => aabbS => aabbaSbS => aabbabS => aabbab
- S =rm=> aSbS => aSbaSbS => aSbaSb => aSbab => aaSbSbab => aaSbbab => aabbab
- Omit
- Ambiguous
- The set of all strings of 'a's and 'b's of the equal number of 'a's and 'b's
7、 Unambiguous, boolean expression
4.2.3
Design grammars for the following languages:
- The set of all strings of 0s and 1s such that every 0 is immediately followed by at least one 1.
- ! The set of all strings of 0s and 1s that are palindromes; that is, the string reads the same backward as forward.
- ! The set of all strings of 0s and 1s with an equal number of 0s and 1s.
- !! The set of all strings of 0s and 1s with an unequal number of 0s and 1s.
- ! The set of all strings of 0s and as in which 011 does not appear as a substring.
- !! The set of all strings of 0s and 1s of the form xy, where x<>y and x and y are of the same length.
Answer
1、
S -> (0?1)*2、
S -> 0S0 | 1S1 | 0 | 1 | ε3、
S -> 0S1S | 1S0S | ε5、
S -> 1*(0+1?)*4.2.4
There is an extended grammar notation in common use. In this notation, square and curly braces in production bodies are metasymbols (like -> or |) with the following meanings:
- Square braces around a grammar symbol or symbols denotes that these constructs are optional. Thus, production A -> X[Y]Z has the same effect as the two productions A -> XYZ and A -> XZ.
- Curly braces around a grammar symbol or symbols says that these symbols may be repeated any number of times, including zero times. Thus, A -> X{YZ} has the same effect as the infinite sequence of productions A -> X, A -> XYZ, A -> XYZYZ, and so on.
Show that these two extensions do not add power to grammars; that is, any language that can be generated by a grammar with these extensions can be generated by a grammar without the extensions.
Proof
| extended grammar | not extended grammar |
|---|---|
| A -> X[Y]Z | A -> XZ | XYZ |
| A -> X{YZ} | A -> XB B -> YZB | ε |
4.2.5
Use the braces described in Exercise 4.2.4 to simplify the following grammar for statement blocks and conditional statements:
stmt -> if expr then stmt else stmt
| if stmt them stmt
| begin stmtList end
stmtList -> stmt; stmtList | stmtAnswer
stmt -> if expr then stmt [else stmt]
| begin stmtList end
stmtList -> stmt [; stmtList]4.2.6
Extend the idea of Exercise 4.2.4 to allow any regular expression of grammar symbols in the body of a production. Show that this extension does not allow grammars to define any new languages.
Proof
Every regular grammar has a corresponding not extended grammar
4.2.7 !
A grammar symbol X (terminal or nonterminal) is useless if there is no derivation of the form S =*=> wXy =*=> wxy. That is, X can never appear in the derivation of any sentence.
-
Give an algorithm to eliminate from a grammar all productions containing useless symbols.
-
Apply your algorithm to the grammar:
S -> 0 | A A -> AB B -> 1
4.2.8
The grammar in Fig. 4.7 generates declarations for a single numerical identifier; these declarations involve four different, independent properties of numbers.
stmt -> declare id optionList
optionList -> optionList option | ε
option -> mode | scale | precision | base
mode -> real | complex
scale -> fixed | floating
precision -> single | double
base -> binary | decimal-
Generalize the grammar of Fig. 4.7 by allowing n options Ai, for some fixed n and for i = 1,2... ,n, where Ai can be either ai or bi· Your grammar should use only 0(n) grammar symbols and have a total length of productions that is O(n).
-
! The grammar of Fig. 4.7 and its generalization in part (a) allow declarations that are contradictory and/or redundant, such as
declare foo real fixed real floating
We could insist that the syntax of the language forbid such declarations; that is, every declaration generated by the grammar has exactly one value for each of the n options. If we do, then for any fixed n there is only a finite number of legal declarations. The language of legal declarations thus has a grammar (and also a regular expression), as any finite language does. The obvious grammar, in which the start symbol has a production for every legal declaration has n! productions and a total production length of O(n x n!). You must do better: a total production length that is O(n2^n)
-
!! Show that any grammar for part (b) must have a total production length of at least 2n.
-
What does part (c) say about the feasibility of enforcing nonredundancy and noncontradiction among options in declarations via the syntax of the programming language?
Answer
1、
stmt -> declare id optionList
optionList -> optionList option | ε
option -> A_1 | A_2 | … | A_n
A_1 -> a_1 | b_1
A_2 -> a_2 | b_2
…
A_n -> a_n | b_n