编译原理(紫龙书)中文第2版习题答案
- 前言
- Exercises for Section 1.1
- Exercises for Section 1.3
- Exercises for Section 1.6
- Exercises for Section 2.2
- Exercises for Section 2.3
- Exercises for Section 2.4
- Exercises for Section 2.6
- Exercises for Section 2.8
- 第2章要点
- Exercises for Section 3.1
- Exercises for Section 3.3
- Exercises for Section 3.4
- Exercises for Section 3.5
- Exercises for Section 3.6
- Exercises for Section 3.7
- Exercises for Section 3.8
- Exercises for Section 3.9
- 第3章要点
- Exercises for Section 4.2
- Exercises for Section 4.3
- Exercises for Section 4.4
- Exercises for Section 4.5
- Exercises for Section 4.6
- Exercises for Section 4.7
- 第4章要点
- Exercises for Section 5.1
- Exercises for Section 5.2
- Exercises for Section 5.3
- Exercises for Section 5.4
- Exercises for Section 5.5
- Exercises for Section 6.1
- Exercises for Section 6.2
- Exercises for Section 6.3
- Exercises for Section 6.4
- Exercises for Section 6.5
- Exercises for Section 6.6
- Exercises for Section 6.7
- Exercises for Section 7.2
- Exercises for Section 7.3
- Exercises for Section 7.4
- Exercises for Section 7.5
- Exercises for Section 7.6
- Exercises for Section 7.7
- Exercises for Section 8.2
- Exercises for Section 8.3
- Exercises for Section 8.4
- Exercises for Section 8.5
- Exercises for Section 12.3
Exercises for Section 7.7
7.7.1
Suppose that the network of objects from Fig.7.20 is managed by an incremental algorithm that uses the four lists Unreached, Unscanned, Scanned, and Free, as in Baker's algorithm. To be specific, the Unscanned list is managed as a queue, and when more than one object is to be placed on this list due to the scanning of one object, we do so in alphabetical order. Suppose also that we use write barriers to assure that no reachable object is made garbage. Starting with A and B on the Unscanned list, suppose the following events occur:
- A is scanned.
- The pointer A -> D is rewritten to be A -> H.
- B is scanned.
- D is scanned.
- The pointer B -> C is rewritten to be B -> I.
Simulate the entire incremental garbage collection, assuming no more pointers are rewritten. Which objects are garbage? Which objects are placed on the Free list?
Answer
-
init
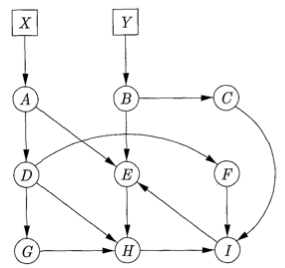
Free = [] Unreached = [C, D, E, F, G, H, I] Uscanned = [A, B] Scanned = [] -
A is scanned.
Unreached = [C, F, G, H, I] Uscanned = [B, D, E] Scanned = [A] -
The pointer A -> D is rewritten to be A -> H.
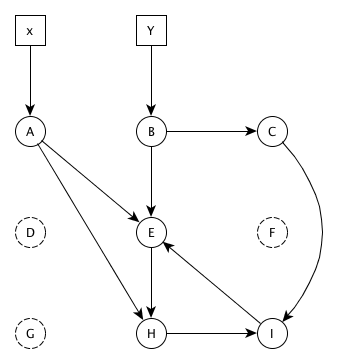
Unreached = [C, F, G, I] Uscanned = [B, D, E, H] Scanned = [A] -
B is scanned.
Unreached = [F, G, I] Uscanned = [D, E, H, C] Scanned = [A, B] -
D is scanned.
Unreached = [F, G, I] Uscanned = [E, H, C] Scanned = [A, B, D] -
The pointer B -> C is rewritten to be B -> I.
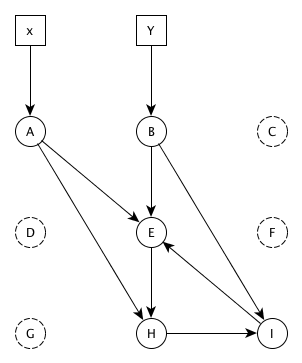
Unreached = [F, G] Uscanned = [E, H, C, I] Scanned = [A, B, D] -
E is scanned.
Unreached = [F, G] Uscanned = [H, C, I] Scanned = [A, B, D, E] -
H is scanned.
Unreached = [F, G] Uscanned = [C, I] Scanned = [A, B, D, E, H] -
C is scanned.
Unreached = [F, G] Uscanned = [I] Scanned = [A, B, D, E, H, C] -
I is scanned.
Unreached = [F, G] Uscanned = [] Scanned = [A, B, D, E, H, C, I] -
end
Free = [F, G] Unreached = [A, B, D, E, H, C, I] Unscanned = [] Scanned = []
so, [C, D, F, G] is garbage, Free list is [F, G].
7.7.2
Repeat Exercise 7.7.1 on the assumption that
- Events (2) and (5) are interchanged in order.
- Events (2) and (5) occur before (1), (3), and (4).
Answer
-
Events (2) and (5) are interchanged in order.
omit
-
Events (2) and (5) occur before (1), (3), and (4).
-
init

Free = [] Unreached = [C, D, E, F, G, H, I] Uscanned = [A, B] Scanned = [] -
The pointer A -> D is rewritten to be A -> H.

Unreached = [C, D, E, F, G, I] Uscanned = [A, B, H] -
The pointer B -> C is rewritten to be B -> I.

Unreached = [C, D, E, F, G] Uscanned = [A, B, H, I] -
A is scanned.
Unreached = [C, D, F, G] Unscanned = [B, H, I, E] Scanned = [A] -
B is scanned.
Unreached = [C, D, F, G] Unscanned = [H, I, E] Scanned = [A, B] -
H is scanned.
Unreached = [C, D, F, G] Unscanned = [I, E] Scanned = [A, B, H] -
I is scanned.
Unreached = [C, D, F, G] Unscanned = [E] Scanned = [A, B, H, I] -
E is scanned.
Unreached = [C, D, F, G] Unscanned = [] Scanned = [A, B, H, I, E] -
end
Free = [C, D, F, G] Unreached = [A, B, H, I, E] Unscanned = [] Scanned = []
so,
[C, D, F, G]is garbage, Free list also is[C, D, F, G]. -
7.7.3
Suppose the heap consists of exactly the nine cars on three trains shown in Fig. 7.30 (i.e., ignore the ellipses). Object o in car 11 has references from cars 12, 23, and 32. When we garbage collect car 11, where might o wind up?
Answer
if any room in trains 2 and 3
o can go in some existing car of either trains 2 and 3.
else
o can go in a new, last car of either trains 2 and 3. 7.7.4
Repeat Exercise 7.7.3 for the cases that o has
- Only references from cars 22 and 31.
- No references other than from car 11.
Answer
-
Only references from cars 22 and 31.
The same with Exercise 7.7.3.
-
No references other than from car 11.
if there is room in car 12 o can go in car 12 else if there is room in other cars of train 1 o can go in any car has room else o can go in a new, last car of train 1
7.7.5
Suppose the heap consists of exactly the nine cars on three trains shown in Fig. 7.30 (i.e., ignore the ellipses). We are currently in panic mode. Object o1 in car 11 has only one reference, from object o2 in car 12. That reference is rewritten. When we garbage collect car 11, what could happen to o1?
Answer
It is not important which train we move it to, as long as it is not the first train?