5.2 节的练习

5.2.1

图 5-7 中的依赖图的全部拓扑顺序有哪些

解答

[ 1, 2, 3, 4, 5, 6, 7, 8, 9 ],
[ 1, 2, 3, 5, 4, 6, 7, 8, 9 ],
[ 1, 2, 4, 3, 5, 6, 7, 8, 9 ],
[ 1, 3, 2, 4, 5, 6, 7, 8, 9 ],
[ 1, 3, 2, 5, 4, 6, 7, 8, 9 ],
[ 1, 3, 5, 2, 4, 6, 7, 8, 9 ],
[ 2, 1, 3, 4, 5, 6, 7, 8, 9 ],
[ 2, 1, 3, 5, 4, 6, 7, 8, 9 ],
[ 2, 1, 4, 3, 5, 6, 7, 8, 9 ],
[ 2, 4, 1, 3, 5, 6, 7, 8, 9 ]

算法见 5.2.1.js

5.2.2

对于图 5-8 中的 SDD，给出下列表达式对应的注释语法分析树：

int a, b , c
float w, x, y, z

解答

int a, b, c

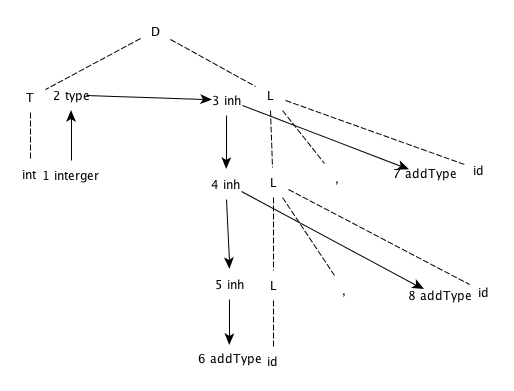
5.2.3

假设我们有一个产生式 A -> BCD。A, B, C, D 这四个非终结符号都有两个属性，综合属性 s 和继承属性 i。对于下面的每组规则，指出（1）这些规则是否满足 S 属性定义的要求（2）这些规则是否满足 L 属性定义的要求（3）是否存在和这些规则一致的求值过程？

A.s = B.i + C.s
A.s = B.i + C.s , D.i = A.i + B.s
A.s = B.s + D.s
! A.s = D.i , B.i = A.s + C.s , C.i = B.s , D.i = B.i + C.i

解答

否，？
否，是
是，是
否，否

5.2.4 ！

这个文法生成了含“小数点”的二进制数：

S -> L.L|L
L -> LB|B
B -> 0|1

设计一个 L 属性的 SDD 来计算 S.val，即输入串的十进制数值。比如，串 101.101 应该被翻译为十进制数 5.625。

解答

	产生式	语法规则
1)	S -> L_1.L_2	L_1.isLeft = true L_2.isLeft = false S.val = L_1.val + L_2.val
2)	S -> L	L.isLeft = true S.val = L.val
3)	L -> L_1B	L_1.isLeft = L.isLeft L.len = L_1.len + 1 L.val = L.isLeft ? L_1.val * 2 + B.val : L_1.val + B.val * 2^(-L.len)
4)	L -> B	L.len = 1 L.val = L.isLeft ? B.val : B.val/2
5)	B -> 0	B.val = 0
6)	B -> 1	B.val = 1

其中：

isLeft 为继承属性，表示节点是否在小数点的左边
len 为综合属性，表示节点包含的二进制串的长度
val 为综合属性

5.2.5 ！！

为练习 5.2.4 中描述的文法和翻译设计一个 S 属性的 SDD。

解答

	产生式	语法规则
1)	S -> L_1.L_2	S.val = L_1.val +　L_2.val/L_2.f
2)	S -> L	S.val = L.val
3)	L -> L_1B	L.val = L_1.val2 + B.val L.f = L_1.f 2
4)	L -> B	L.val = B.val L.f = 2
5)	B -> 0	B.val = 0
6)	B -> 1	B.val = 1

5.2.6 ！！

使用一个自顶向下的语法分析文法上的 L 属性 SDD 来实现算法 3.23。这个算法把一个正则表达式转换为一个 NFA。假设有一个表示任意字符的词法单元 char，并且 char.lexval 是它所表示的字符。你可以假设存在一个函数 new()，该函数范围一个新的状态页就是一个之前尚未被这个函数返回的状态。使用任何方便的表示来描述这个 NFA 的翻译。