Exercises for Section 8.5

8.5.1

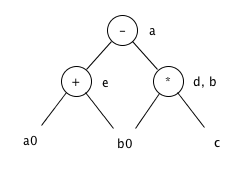
Construct the DAG for the basic block

d = b * c
e = a + b
b = b * c
a = e - d

Answer

8.5.2

Simplify the three-address code of Exercise 8.5.1, assuming

1. Only a is live on exit from the block.
2. a, b, and c are live on exit from the block.

Answer

1. Only a is live on exit from the block.

    e = a + b
    d = b * c
    a = e - d

2. a, b, and c are live on exit from the block.

    e = a + b
    b = b * c
    a = e - b

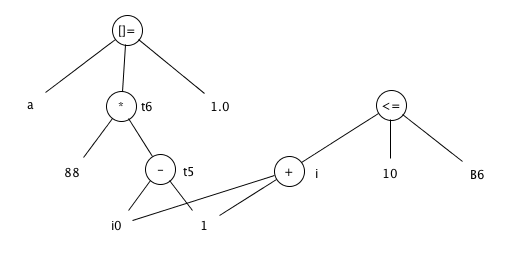
8.5.3

Construct the basic block for the code in block B6 of Fig. 8.9. Do not forget to include the comparison i <= 10.

Answer

疑问

• “Construct the basic block” 被翻译成 “构造 DAG”，是这个意思吗？
• 如何为一个 “if goto” 语句 construct the basic block？

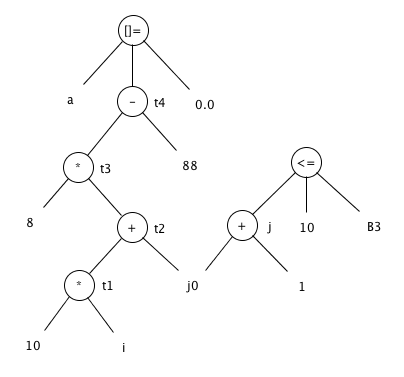
8.5.4

Construct the DAG for the code in block B3 of Fig. 8.9.

Answer

8.5.5

Extend Algorithm 8.7 to process three-statements of the form

1. a[i] = b
2. a = b[i]
3. a = *b
4. *a = b

8.5.6

Construct the DAG for the basic block

a[i] = b
*p = c
d = a[j]
e = *p
*p = a[i]

on the assumption that

1. p can point anywhere.
2. p can point only to b or d.

疑问

8.5.6 节讲指针赋值这里又没有 demo 啊！！！

• *p = c 和 c = *p翻译成 DAG 是不是这样的：
• *p = a[i] 这样的语句用 DAG 如何表示？
• 8.5.6 节讲到：the operator =* must take all nodes that are currently associated with identifiers as arguments。这句话再 DAG 中如何表示？

8.5.7 !

If a pointer or array expression, such as a[i] or *p is assigned and then used, without the possibility of being changed in the interim, we can take advantage of the situation to simplify the DAG. For example, in the code of Exercise 8.5.6, since p is not assigned between the second and fourth statements,the statement e = *p can be replaced by e = c, regardless of what p points to. Revise the DAG-construction algorithm to take advantage of such situations, and apply your algorithm to the code of Example 8.5.6.

8.5.8

Suppose a basic block is formed from the C assignment statements

x = a + b + c + d + e + f;
y = a + c + e;

1. Give the three-address statements (only one addition per statement) for this block.
2. Use the associative and commutative laws to modify the block to use the fewest possible number of instructions, assuming both x and y are live on exit from the block.

Answer

1. three-address statements

    t1 = a + b
    t2 = t1 + c
    t3 = t2 + d
    t4 = t3 + e
    t5 = t4 + f
    x = t5
    t6 = a + c
    t7 = c + e
    y = t6 + t7

2. optimized statments

    t1 = a + c
    t2 = t1 + e
    y = t2
    t3 = t2 + b
    t4 = t3 + d
    t5 = t4 + f
    x = t5